The denominator becomes ab ab a2 b2 which simplifies to 927. Limits of function factoringbeginarrayla sqrt a cdot sqrt a a - b sqrt a - sqrt b sqrt a sqrt b A2 - B2 A - BA B.

How To Find A Harmonic Conjugate Complex Analysis Complex Analysis Analysis Math Videos
A-bsqrtn This has the property that.

Conjugate square root. Note that sqrtxi2 sqrtx2i2 x-1 -x Putting these facts together we have the conjugate of sqrt-20 as. In particular the conjugate of a root of a quadratic polynomial is the other root obtained by changing the sign of the square root appearing in the quadratic formula. A conjugate surd is a sum and the difference between two simple quadratic surds.
The conjugate of an expression is identical to the original expression except that the sign between the terms is changed. In particular the conjugate of a root of a quadratic polynomial is the other root obtained by changing the sign of the square root appearing in the quadratic formula. Absqrtna-bsqrtn a2-n b2 hence is often used to rationalise denominators.
The complex conjugate is similar to the radical conjugate but with n -1. So to simplify 44 2 root 3 multiply both the numerator and denominator by 4 2 root 3 to get rid of the radical in the denominator. Using the complex conjugate root theorem find all of the remaining zeros the roots of each of the following polynomial functions and write each polynomial in root factored form.
There is a formula for the square root of a complex number see Wikipedia. The radical conjugate of sqrt8 is -sqrt8. Given a real number x0 we have sqrt-x sqrtxi.
What is the radical root theorem. Given 2i is one of the roots of fx x3 3x2 4x 12 find its remaining roots and write fx in root factored form. In mathematics the conjugate of an expression of the form displaystyle absqrt d is displaystyle a-bsqrt d provided that displaystyle sqrt d does not appear in a and b.
Conjugates Dividing by Square Roots. We can multiply both top and bottom by 32 the conjugate of 32 which wont change the value of the fraction. One says also that the two expressions are conjugate.
3 5 3 6 left sqrt 3 sqrt 5rightleft sqrt 3 - sqrt 6right 3. Imaginary part of a complex number Conjugate square roots the change of sign of a square root in an expression Conjugate element field theory a generalization cube root and a pair of complex conjugate cube roots and all nonzero complex numbers have three distinct complex cube roots For example the real cube root non - real complex roots come in conjugate pairs there are. A i b a a 2 b 2 2 i sgn b a a 2 b 2 2 So if b b assuming b to be strictly positive then.
Suppose 32 and 5 are two simple quadratic surds then the conjugate surds can be written using the sum and the difference of these surds as 32 5 and 32 5 respectively. If sqrtn is irrational and a b are rational numbers then the radical conjugate of. Conjugate surds are also known as complementary surds.
Are rational the Conjugate Radical Roots theorem states that if the equation px0 has a root of the form xstu where u is rational then the. One says also that the two expressions are. 1 32 32 32 32 32 22 32 7.
Normalsize Complex conjugate and absolute value. For example the conjugate of 4 2 root 3 is 4 2 root 3. This video provides examples of how to multiply binomial radical conjugates that involving square rootsVideo Library.
Conjugate square roots This article is about conjugation by changing the sign of a square root. Complex conjugation is the special case where the square root is mathdisplaystyle isqrt-1. What is the conjugate of a square root.
Move the square root of 2 to the top1 32. Conjugate surds are also known as complementary surds. 2 absolute value abisqrta2b2 Customer Voice.
Given a complex number zabi where a b in RR and i sqrt-1 the complex conjugate or conjugate of z denoted barz or z is given by barz a-bi. For other uses see Conjugate disambiguation. Thanks A2A Note that in mathematics the conjugate of a complex number is that number which has same real and imaginary parts but the sign of imaginary part is opposite ie The conjugate of number a ib is a - ib The conjugate of number a -.
Then I set the original expression equal to the last line from the multiplication above and complete the calculations by simplifying each term.
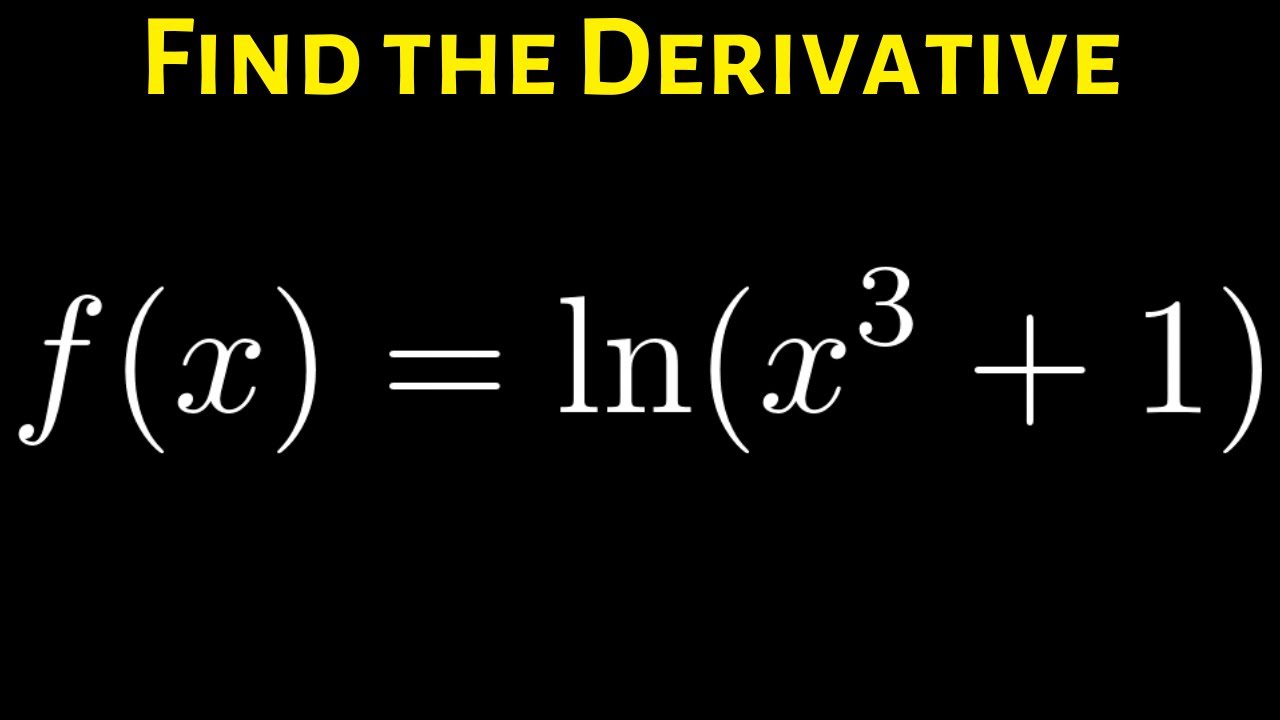
How To Find The Derivative Of F X Ln X 3 1 Using The Chain Rule Chain Rule Math Videos F X

Conjugates Inb Notes Teaching Algebra Math Methods High School Math

A Technique Is Just A Trick That Went Viral Math Tutorials Maths Exam Techniques

Limit Of An Irrational Function With A Square Root Term Term Square Roots Function

Calculus Problem Limit Of A Rational Function With 0 0 Indeterminate Form Rational Function Calculus Denominator

Rbse Solutions For Class 11 Maths Chapter 5 Complex Numbers Ex 5 1 Rbsesolutions Rbseclass11maths Rajasthanboardclas Complex Numbers Math Solving Equations

Limit Of The Irrational Function 1 X Sqrt 63 X 2 8 At X 1 Problem And Solution Calculus Function

Solving Limits Analytically Math Equations Solving Math

Calculus Problem Find The Limit Of An Irrational Function Calculus Youtube Wholeness

Adding And Subtracting Radicals Bingo Freebie Adding And Subtracting Subtraction Math Resources

This Solution Shows The Simplification Of The Complex Numbers Using The Conjugate Of Its Denominator Therefore Complex Numbers Algebra Lessons Denominator

The Derivative Product Rule Derivative Calculus

The Product Rule Find The Derivation Of A Trigonometric Function Product Rule Trigonometric Functions Rules

Solving Quadratics By Factoring And Completing The Square She Loves Math Solving Quadratics Quadratics Solving Equations

Find The Conjugate Complex Numbers Math Practice Worksheets Number Worksheets

Limit Of An Irrational Function With A Square Root Term Square Roots Term Limits

A Technique Is Just A Trick That Went Viral Friends Quotes Techniques Math



